双曲螺线?别慌,让我来给你画个“龙”!
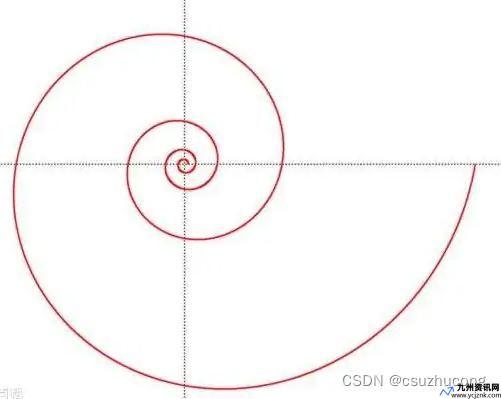
嘿,小伙伴们!今天咱们来聊聊双曲螺线这个有趣的东西。别看它名字听起来有点高冷,其实画起来还挺简单的,就像画个“龙”一样!
你要知道,双曲螺线其实就是一种曲线,它在极坐标系里可以用公式表示。这个公式嘛,就是 ρ = a/θ,简单吧?
ρ 代表的是极径,就是从极点到曲线上某一点的距离。
θ 代表的是极角,就是从极轴到极径的夹角。
a 则是常数,它决定了螺线的形状和大小。
看到这个公式,是不是感觉有点晕?别怕!咱们慢慢来,先来理解一下它长什么样。
想象一下,你在一个圆盘上画一条线,这条线从圆心开始,绕着圆心旋转。你还需要一个点,这个点沿着这条线移动,而且它移动的速度与旋转的角度成反比。也就是说,旋转角度越大,移动的速度就越慢。
当这个点沿着这条线移动时,它所经过的轨迹就是一条双曲螺线!
是不是有点抽象?没关系,我给你画个图你就明白了:
| 极角 | 极径 | 坐标 |
|---|---|---|
| 0 | (∞, 0) | |
| π/4 | 4a/π | (4a/π, π/4) |
| π/2 | 2a/π | (2a/π, π/2) |
| π | a/π | (a/π, π) |
| 3π/2 | 2a/(3π) | (2a/(3π), 3π/2) |
| 2π | a/(2π) | (a/(2π), 2π) |
这个表格列出了几个点,你可以根据这些点在极坐标系里画出来,就能得到一条双曲螺线了。当然,你可以画更多的点,这样得到的曲线就更加精确。
你看,双曲螺线其实就是一条不断绕着圆心旋转,并且越来越靠近一条直线的曲线。这条直线就是双曲螺线的渐近线。
那什么是渐近线呢?
想象一下,你正在追赶一辆汽车,你和汽车之间越来越近,但是永远无法追上它。这个距离就好像渐近线一样,它越来越靠近曲线,但是永远不会与曲线相交。
对于双曲螺线来说,它的渐近线就是直线 y = a,也就是说,当 θ 趋近于 0 或 2π 时,曲线上的点会越来越靠近这条直线。
双曲螺线到底有什么用呢?
别以为它只是个数学概念,它在现实生活中可是很有用的!比如:
机械设计: 双曲螺线可以用来设计螺旋状的齿轮、弹簧等机械零件,因为它的形状可以确保零件之间的啮合。
艺术设计: 双曲螺线独特的形状,可以应用于各种艺术设计中,比如服装、家具等。
自然界: 一些植物的叶片、海螺的螺旋形外壳,都可以用双曲螺线来模拟。
怎么样,是不是觉得双曲螺线其实挺有意思的?
现在,轮到你发挥想象力了!
你能不能用双曲螺线来画一些独特的图案?或者,你能不能在生活中找到一些与双曲螺线相关的例子?
来吧,一起分享你的创意吧!