哎呦喂,老铁们,今天咱们来聊聊一个“老生常谈”的那就是sin60°等于多少?别看这只是一道简单的三角函数题,它可是数学世界里的“明星”,经常出现在各种考试和学习资料中。
咱们得明确一点,sin60°可不是什么神秘代码,它指的是60度角的正弦值,也就是在直角三角形中,60度角所对应的对边长度与斜边长度的比值。
那这个比值到底是多少呢?别急,让我来给你慢慢道来。
正弦函数的来龙去脉
其实,正弦函数的历史可以追溯到古希腊时期,当时人们用它来研究天体的运动规律。后来,随着数学的发展,正弦函数被广泛应用于各种领域,比如工程、物理、建筑等等。
简单来说,正弦函数就是用来描述一个角的“正弦”变化的,它就像一个“能量”值,反映了角的大小与对边和斜边的关系。
揭开sin60°的面纱
现在,我们终于要揭开sin60°的面纱了!
我们需要一个特殊的直角三角形,这个三角形的三个角分别是30度、60度和90度,俗称“30-60-90三角形”。
根据勾股定理,我们可以推导出这个三角形的边长关系:
| 角 | 对边 | 邻边 | 斜边 |
|---|---|---|---|
| 30° | 1 | √3 | 2 |
| 60° | √3 | 1 | 2 |
| 90° | 2 | 1 | √3 |
所以,sin60°等于60度角所对应的对边长度(√3)除以斜边长度(2),也就是:
sin60° = √3 / 2
记忆小技巧
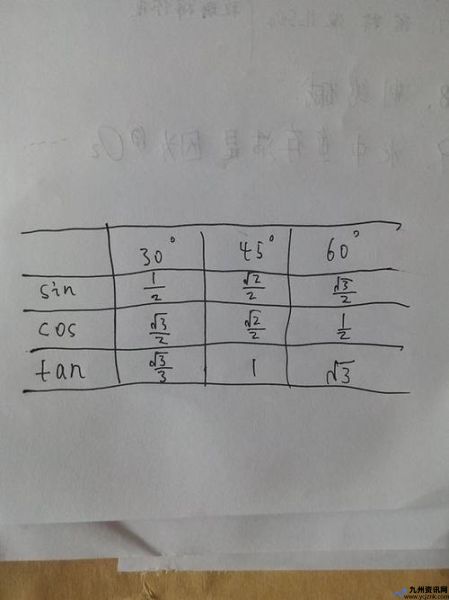
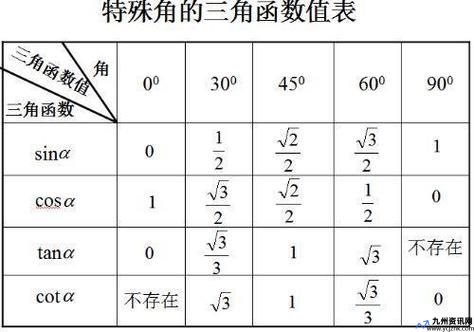
记住sin60°=√3/2,其实有一个很简单的小技巧,那就是“30、45、60”。
30°: sin30° = 1/2
45°: sin45° = √2 / 2
60°: sin60° = √3 / 2
看到没,这三个值都是以2为分母,分子分别是1、√2、√3,是不是很好记?
sin60°的应用
那么,sin60°在现实生活中有什么应用呢?
建筑学: 建筑师可以用正弦函数来计算建筑物的斜坡角度,例如屋顶的坡度。
物理学: 物理学家可以用正弦函数来研究振动和波动的现象,例如声波、光波等等。
工程学: 工程师可以用正弦函数来设计各种机械设备,例如发动机、桥梁等等。
总结
sin60°=√3/2,这是一个重要的三角函数值,在数学和现实生活中都有着广泛的应用。希望这篇文章能够帮助你更好地理解它,下次遇到它,就不用再慌慌张张了!
你还知道哪些关于三角函数的有趣知识?不妨在评论区分享一下吧! 😉